快速排序使用分治法实现，即一个一个复杂的问题分解为一系列容易解决的小问题，最终得到问题的解。

算法步骤

快速排序的三步分治过程：例如对 A[p..r] 进行快速排序

分解：数组 A[p..r] 被划分为两个(可能为空)子数组 A[p…q-1] 和 A[p+1…r]，使得A[p…q-1] 中的每一个元素都小于 A[q]，而 A[q] 也小于等于 A[q+1…r]中的每个元素。其中，计算下标 q 也是划分过程的一部分。
解决：通过递归调用快速排序，对子数组A[p…q-1] 和 A[p+1…r] 进行排序。
合并：因为子数组都是原址排序，所以不需要合并操作，数组A[p…r]已经有序

c++ 代码实现

int partition(vector<int> &A, int low,int high){
    // 将 q 作为基准，小于 q 的移到左边，大于 q 移动右边
    int q = A[low];   //  A[low] 的值现在保存在 q 中，所以A[low] 可以作为空位   

    while(low<high){
        while(low<high && A[high]>=q){
            // 从右往左找，找到一个小于等于 q 的值
            --high;
        }
        A[low] = A[high];  // 将找到的值移动到 A[low], A[high] 移动到了A[low]，此时A[high] 可以作为空位
        while (low < high && A[low] <= q)
        {
            // 从左往右找，找到一个大于等于 q 的值 
            ++low;
        }
        A[high] = A[low];  // 将找到的值移动到 A[high]，此时A[low] 可以作为空位
    }
    // 当 low==high 时退出循环，A[low]作为空值，存储 q
    A[low] = q;
    return low;
}

void qsort(vector<int>&A,int low,int high){
    if(low < high){
        int q = partition(A, low, high); 
        qsort(A,low,q-1);
        qsort(A,q+1,high);
    }
}

void qsort(vector<int>&A,int low,int high){
    if(low < high){
        int q = partition(A, low, high);  // 将数组划分为 左右两个子数组，满足左边数组的每个元素都小于等于右边数组元素
        qsort(A,low,q-1);
        qsort(A,q+1,high);
    }
}

int main(){
    vector<int>vec = {2,4,3,5,6,2,3,1,2,3,1,2,3,2,-2,3,2};
    qsort(vec,0,vec.size()-1);
    for(auto &x:vec){
        cout<<x<<" ";
    }
    return 0;
}

时间复杂度分析

快速排序的运行时间依赖于划分是否平衡，而平衡与否又依赖于划分的元素。如果划分是平衡的，那么快速排序算法性能与归并排序一样。如果划分是不平衡的，那么快速排序的性能就接近于插入排序。

最坏情况划分

当划分产生的两个子问题分别包含了 n-1 个元素和 0 个元素时，便是快速排序的最坏情况。

算法运行时间的递归式可以表示为: T(n) = T(n-1)+T(0)+Θ(n)，每一层递归的代价可以被累加起来，从而得到一个前n项和(或称级数)，其结果为 Θ(n²)。实际上，利用带入法可以直接得到递归式 T(n) = T(n-1)+Θ(n)的解为 T(n) = Θ(n²)。

因此，如果在算法的每一层递归上，划分都是最大程度不平衡，那么算法的时间复杂度就是 Θ(n²)。也就是说，在最坏情况下，快速排序的运行时间并不比插入排序更好。此外，当输入数组已经完全有序时，快速排序的时间复杂度仍然为 Θ(n²)。而在同样的情况下，插入排序的时间复杂度为 O(n)。

最好情况划分

在可能的最平衡的划分中，partition 得到的两个子问题的规模都不大于 n/2。在这种情况下，快速排序的性能非常好。此时，算法运行时间的递归式为：T(n) = T(n-1) + Θ(n)，该递归式的解为 Θ(nlgn)。通过在每一层中都平衡划分子数组，我们得到了一个渐近时间更快的算法。

平衡的划分

快速排序的平均运行时间更接近于其最好情况，而非最坏情况。

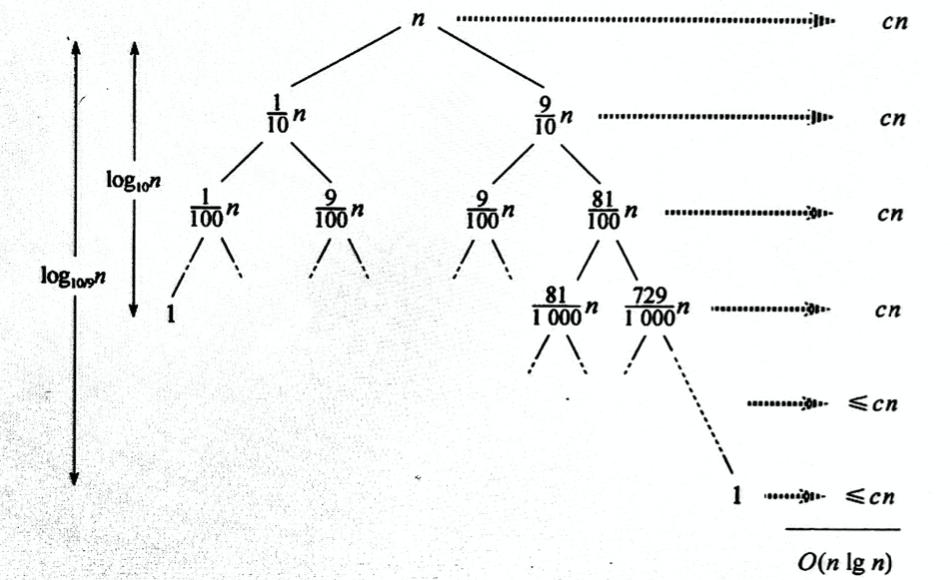
例如：假如划分算法总是产生9:1的划分，乍一看，划分很不平衡。此时，我们得到的快速排序时间复杂度的递归式为：T(n) = T(9n/10) + T(n/10) + cn。下图显示了这一递归调用所对应的递归树。注意，树中每一层的代价都是 cn，直到深度 $lg n$ = Θ(lg n)处到达递归的边界条件为止。快速排序的总代价为 O(nlgn)

总结

快速排序时间复杂度：

平均情况 O(nlgn)
最优情况 O(nlgn)
最坏情况 O(n²)

空间复杂度 O(lg(n))

使用随机数来确定一个基准数，可以使划分左右序列更加合理。

随机优化版本

#include <vector>
#include <iostream>
#include <random>
using namespace std;

int partition(vector<int> &A, int low,int high){
    random_device rd;                // 随机数种子，每次运行都会生成不同的随机bit流
    default_random_engine eng(rd()); // 生成随机的bit流
    uniform_int_distribution<int> dis(low, high); // 通过调用产生dis(eng) 产生[low,high] 之间的随机数，包括边界low,high
    int id = dis(eng);
    swap(A[low], A[id]);

    // 将 q 作为基准，小于 q 的移到左边，大于 q 移动右边
    int q = A[low];   //  A[low] 的值现在保存在 q 中，所以A[low] 可以作为空位   
   
    while(low<high){
        while(low<high && A[high]>=q){
            // 从右往左找，找到一个小于等于 q 的值
            --high;
        }
        A[low] = A[high];  // 将找到的值移动到 A[low], A[high] 移动到了A[low]，此时A[high] 可以作为空位
        while (low < high && A[low] <= q)
        {
            // 从左往右找，找到一个大于等于 q 的值 
            ++low;
        }
        A[high] = A[low];  // 将找到的值移动到 A[high]，此时A[low] 可以作为空位
    }
    // 当 low==high 时退出循环，A[low]作为空值，存储 q
    A[low] = q;
    return low;
}

void qsort(vector<int>&A,int low,int high){
    if(low < high){
        int q = partition(A, low, high); 
        qsort(A,low,q-1);
        qsort(A,q+1,high);
    }
}

int main(){
    vector<int>vec = {2,4,3,5,6,2,3,1,2,3,1,2,3,2,-2,3,2};
    qsort(vec,0,vec.size()-1);
    for(auto &x:vec){
        cout<<x<<" ";
    }
    return 0;
}

参考

《算法导论》

编程之禅

快速排序分析及优化