编程之禅
0%

归并排序原理

发表于 更新于 分类于 阅读次数： Disqus：

归并排序属于分治法思想，归并排序完全遵循分治模式。直观上其操作如下：

  • 分解：分解待排序的n个元素成各具n/2个元素的两个子序列。
  • 解决：使用归并排序递归地排序两个子序列。
  • 合并：合并两个已排序的子序列以产生已排序的数组。

核心函数有两个，merge(A,p,q,r)：将已经有序的序列 A[p…q]和A[q+1,r] 合并为一个有序序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
#include <climits>
using namespace std;

void merge(vector<int> &A, int p, int q, int r)
{
    int n1 = q - p + 1;
    int n2 = r - q;
    vector<int> L(n1 + 1);
    vector<int> R(n2 + 1);
    L[n1] = INT_MAX;
    R[n2] = INT_MAX;
    for (int i = 0; i < n1; ++i)
    {
        L[i] = A[p + i];
    }
    for (int i = 0; i < n2; ++i)
    {
        R[i] = A[q + i + 1];
    }
   
    int i = 0, j = 0;
    for (int k = p; k <= r; ++k)
    {
        if (L[i] <= R[j])
        {
            A[k] = L[i];
            ++i;
        }
        else
        {
            A[k] = R[j];
            ++j;
        }
    }
}

void merge_sort(vector<int> &A, int p,int r){
    if(p<r){
        int q = (p+r)>>1;   // (p+r)/2
        merge_sort(A,p,q);
        merge_sort(A,q+1,r);
        merge(A,p,q,r);
    }
}

int main()
{
    vector<int> A{1,5,2,7,3,7,1,6,3};
    merge_sort(A,0,A.size()-1);
    for(auto x:A){
        cout<<x<<" ";
    }
    return 0;
}

分治法时间复杂度分析

假设 T(n) 是规模为 n 的一个问题的运行时间。把原问题分解为 a 个子问题，每个子问题的规模为原问题的 1/b（对于归并排序，a和b都是2）。为了求解一个规模为 n/b 的子问题，需要 T(n/b)，所以需要aT(n/b)的时间来求解a个子问题。如果分解问题成子问题需要时间 D(n)，合并子问题为原问题的解需要时间 C(n)，那么得到以下递归式：T(n) = aT(n/b) + D(n) + C(n)

归并排序算法

时间复杂度

分解：只需计算数组中间的下标位置，需要常量时间，D(n) = O(1)

解决：我们递归地求解两个规模为 n/2 的子为题，将产生 2T(n/2) 的时间

合并：排序两个有序数组，需要线性时间，C(n) =Θ(n)，为什么这里用Θ，而不用 O，因为 O(n)还包括常数时间，Θ(n)不包括常数时间。

T(n) = Θ(1) 当n==1

T(n) = 2T(n/2) + Θ(n) 当 n >1

以下为 T(n)的递归树：

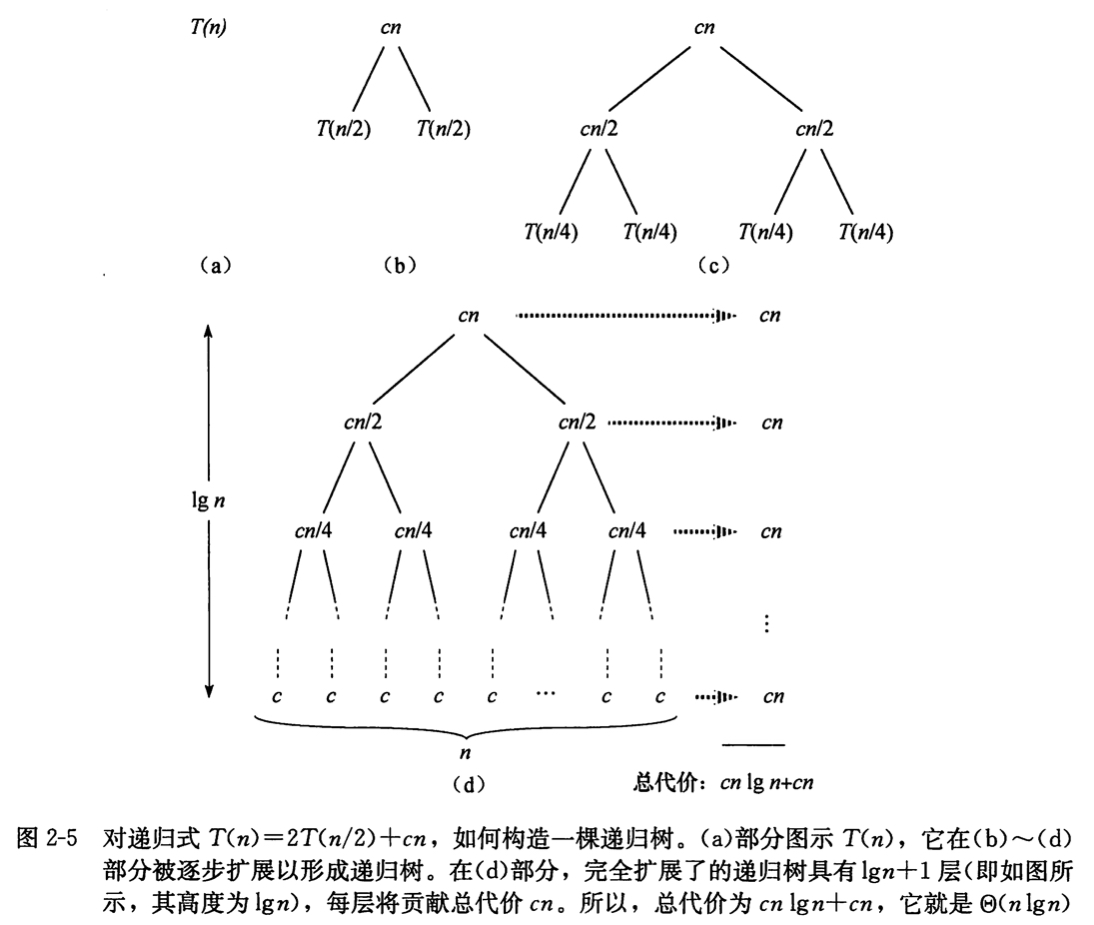
IMG_082FCEFC406D-1

顶层具有总代价 cn，下一层具有总代价 c(n/2)+c(n/2) == cn，下一层的下一层具有总代价 c(n/4)+c(n/4)+c(n/4)+c(n/4) == cn。总的来说，递归树每一层的代价都为 cn

递归树的总的层数为 lgn+1，其中 n是叶数，对应输入规模。总的代价为 cn( lgn+1) = cn$\lg n$​+cn。忽略低阶项和常量 c，最终归并排序的时间复杂度为 O(n lgn)。

空间复杂度

递归树的深度为 lgn+1，每次递归使用常量空间 O(1)

使用两个零时数组，空间复杂度为 O(n)

所以总的空间复杂度为 O(n + 1*(lgn+1) )，忽略低阶项和常数项 1，最终空间复杂度为 O(n)