插入排序原理

原理

对于少数元素的排序，这是一个有效算法。插入排序类似于排序手中的扑克牌。开始时，我们左手为空并且桌子上的牌面向下。然后我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。

假设每个人发10张扑克牌，我们使用for循环来遍历每一张需要拿起的牌。

每拿起一张牌，我们都从右往左，依次与手中的每张牌比较，若大于刚拿起的牌，则将它往后移一位，移位之后就有空缺的位置，若不大于，则将它插入空缺的位置上。

代码实现

void insertion(vector<int> &nums){
    for(int i=1; i<nums.size(); ++i){
      	//i代表第i个数字将要插入已排好序的序列中
        int key = nums[i];   //用key来暂存需要插入的数字
        int j = i-1;         //用j来遍历有序数组中从右到左的每个数，直到找到一个数组中小于k的值tem，然后将key值插入tem的右边。若没找到，则将key插入到有序数组最左边
        while(j>-1 && nums[j]>key){
            nums[j+1] = nums[j];  //因为第i个数已经保存在key中，相当于空出来一个位置，如果nums[j]>key，则将它右移一位
            --j;
        }
        nums[j+1] = key; //跳出了while循环，说明已经找到了key值的正确位置
    }
}

复杂度分析

空间复杂度：O(1)。插入排序为原址排序，只用了常数个空间

当数组按逆序排列时，例如(6,5,4,3,2,1)，每个元素需要平均移动步数最多，总的移动步数为闭区间[1,n-1]所有元素的和。根据等差数列前项和公式。

总的移动步数为：

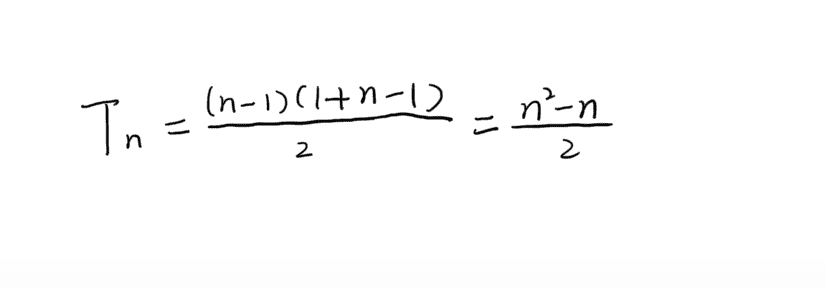
时间复杂度：O(n²)。