B树 B+树 B*树区别
B树的性质
(1)B树的每个节点 x 都具有以下属性:
-
x.n 存储在节点 x 中的关键字个数。
-
x.n 个关键字本身 x.key0, x.key1,…, x.keyn-1,以升序排列,注编程语言数组下标从 0 开始。
-
x.leaf 布尔值,表示节点 x 是否是叶节点。
(2)B树的每个内部节点具有以下属性:
- 包含 x.n+1 个指向其孩子的指针 x.c0,x.c1,…,x.cn,叶节点没有孩子节点,它们的 ci 属性值未定义。
(3)关键字 x.keyi对子树节点中的关键字进行分割,如果 ki为任意一个存储在以 x.ci为根的子树中的关键字,那么:k1<=x.key1<=k2<=…<=x.keyn<=kx.n+1,如下图所示:
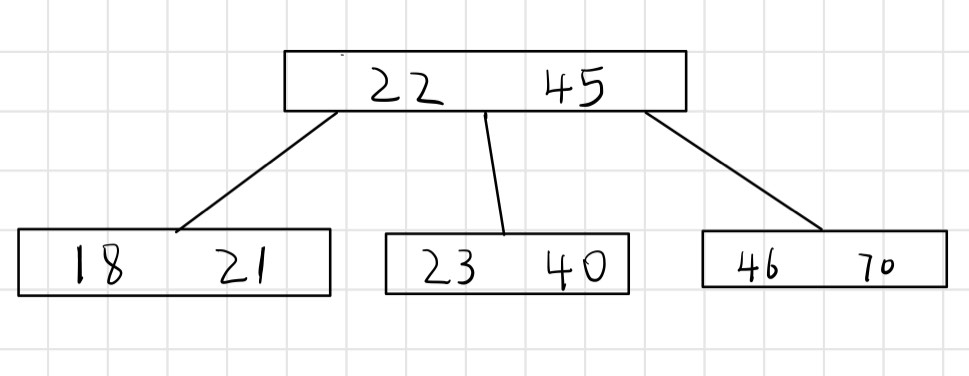
(4)每个叶节点具有相同的深度,即树的高度 h
(5)每个节点所包含的关键字个数有上界和下界,用一个被称为B树的最小度数的固定整数 t>=2 来表示这些界:
-
下界:除了根节点以外的每个节点必须至少有 t-1 个关键字。除了根节点和叶子节点以外的每个节点至少有 t 个孩子。如果树非空,根节点至少有 1 个关键字。
-
上界:每个节点至多可包含 2t-1 个关键字,一个内部节点(非叶子节点)至多可有 2t 个孩子。当一个节点有 2t-1 个关键字时,称该节点为满的。
-
t 值越大,B树的高度就越小。
查找时间复杂度
每个节点的遍历所有关键字值时间为 O(t),搜索路径构成B树的一条简单路径,所以总的时间复杂度为 O(t$\log_t{n}$)
插入时间复杂度
插入用到一个辅助过程,insertNonFull :向非满的节点中插入关键字。insert 需要访问的节点数为 O(h),每次调用 insertNonFull 的时间复杂度为 O(1),所以总的时间复杂度为 O(t$\log_t{n}$)
删除时间复杂度
需要访问节点个数 O(h),总的时间复杂度为 O(th) == O(t$\log_t{n}$)
B+树的性质
B+ 树由B树改进而来,具有以下不同于 B树的性质:
(1)B 树的每个节点都包含数据和索引,B+树只在叶节点中存储数据,内部节点只存储索引。如下图所示:
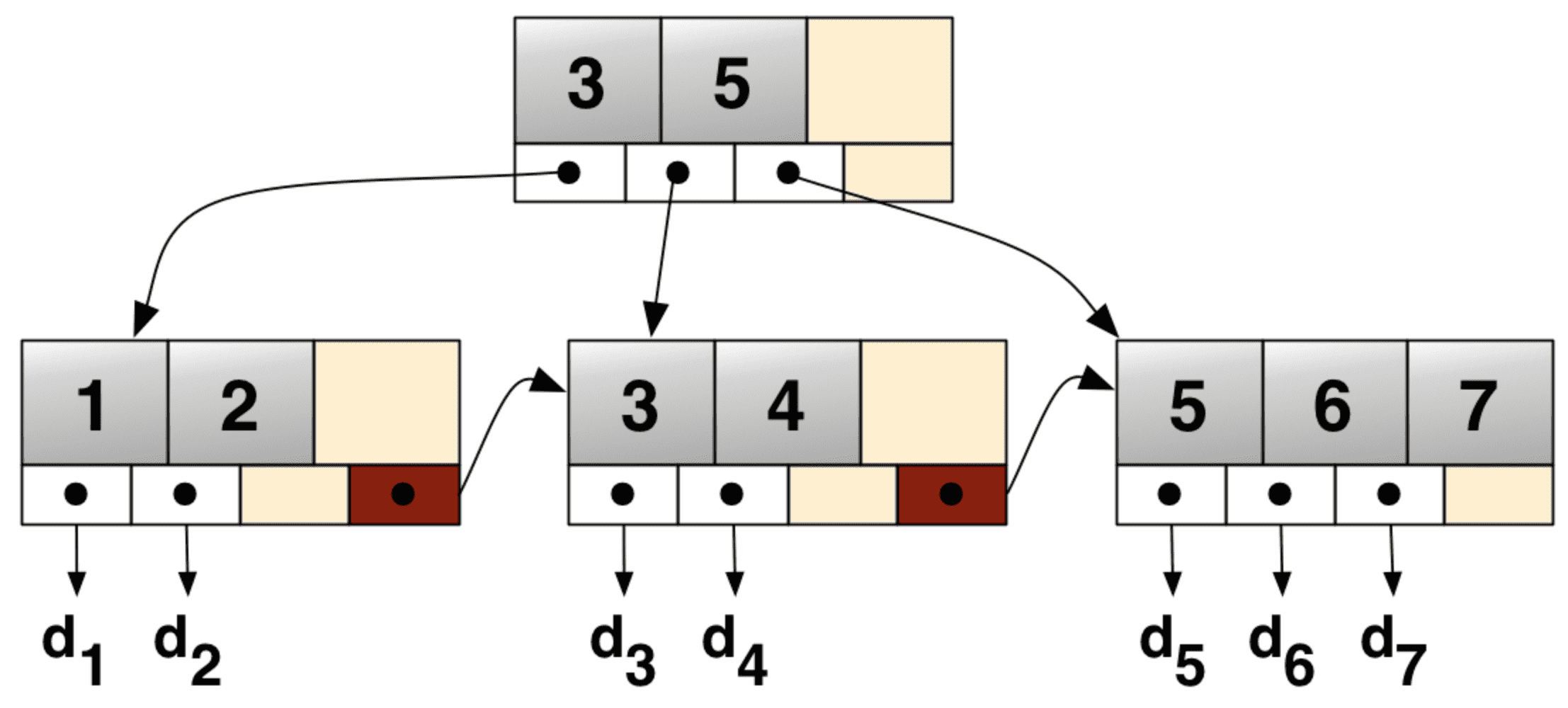
注:内部节点 3 和 5 并不是关键字,它用来界定关键字的范围。
(2)B+树的叶子节点按升序排序,所有叶子节点构成一个链表。
B+树具有以下优点:
- 单一节点存储的元素更多,使得查询的IO次数更少,平衡操作不经常发生,而且效率增加了,适合做为数据库MySQL的底层数据结构。
- 所有关键字都位于叶节点,查询更稳定,因为内存地址是连续的,用树的遍历去做范围查找,会不断在树中进行跳跃,即不断在内存中进行跳跃,会造成性能损失。
- 在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
- 所有叶子节点构成一个链表,数据遍历更快。
B*树的性质
B*树是B+树的变种。具有以下不同于 B+树的性质。
-
B*树,除根节点以外的内部节点,关键字个数至少为 3/2满,即 (2t-1)*2/3,向上取整。
-
所
-
而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移关键字,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的关键字创建一个新的节点出来。
参考
面试官问你B树和B+树,就把这篇文章丢给他 - SegmentFault 思否